Singular Value Decomposition - Properties of Symmetric Matrices 2

Geometrical interpretation of eigendecomposition ¶

In the previous post, we showed how to express a symmetric matrix as the product of three matrices, a process known as eigendecomposition. In this post, we revisit this procedure, but from a geometrical perspective.

To begin, let’s assume that a symmetric matrix $\mathbf{A}$ has $n$ eigenvectors, and each eigenvector $\mathbf{u}_i$ is an $n \times 1$ column vector

$$ \begin{equation*} \mathbf{u}_i = \begin{bmatrix} u_{i1} \\ u_{i2} \\ \vdots \\ u_{in} \\ \end{bmatrix} \end{equation*} $$

then the transpose of $\mathbf{u}_i$ is a $1 \times n$ row vector

$$ \begin{equation*} \mathbf{u}_i^T = \begin{bmatrix} u_{i1} & u_{i2} & \ldots & u_{in} \\ \end{bmatrix} \end{equation*} $$

and their multiplication

$$ \begin{equation*} \mathbf{u}_i\mathbf{u}_i^T = \begin{bmatrix} u_{i1} \\ u_{i2} \\ \vdots \\ u_{in} \\ \end{bmatrix} \begin{bmatrix} u_{i1} & u_{i2} & \ldots & u_{in} \\ \end{bmatrix} = \begin{bmatrix} u_{i1}u_{i1} & u_{i1}u_{i2} & \ldots & u_{in}u_{in} \\ u_{i2}u_{i1} & u_{i2}u_{i2} & \ldots & u_{i2}u_{in} \\ \vdots & \vdots & \vdots & \vdots \\ u_{in}u_{i1} & u_{in}u_{i2} & \ldots & u_{in}u_{in} \\ \end{bmatrix} \end{equation*} $$

becomes an $n \times n$ matrix.

Let’s return to $\mathbf{A} = \mathbf{P}\mathbf{D}\mathbf{P}^\top$. First, we calculate $\mathbf{D}\mathbf{P}^\top$ to simplify the eigendecomposition equation:

$$ \begin{align*} \begin{bmatrix} \lambda_1 & 0 & \ldots & 0 \\ 0 & \lambda_2 & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \ldots & \lambda_n \\ \end{bmatrix} \begin{bmatrix} \mathbf{u}_1^\top \\ \mathbf{u}_2^\top \\ \ldots \\ \mathbf{u}_n^\top \\ \end{bmatrix} &= \begin{bmatrix} \lambda_1 & 0 & \ldots & 0 \\ 0 & \lambda_2 & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \ldots & \lambda_n \\ \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & \ldots & u_{1n} \\ u_{21} & u_{22} & \ldots & u_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ u_{n1} & u_{n2} & \ldots & u_{nn} \\ \end{bmatrix} \\ &= \begin{bmatrix} \lambda_1u_{11} & \lambda_1u_{12} & \ldots & \lambda_1u_{1n} \\ \lambda_2u_{21} & \lambda_2u_{22} & \ldots & \lambda_2u_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ \lambda_nu_{n1} & \lambda_nu_{n2} & \ldots & \lambda_nu_{nn} \\ \end{bmatrix} = \begin{bmatrix} \lambda_1\mathbf{u}_1^\top \\ \lambda_2\mathbf{u}_2^\top \\ \ldots \\ \lambda_n\mathbf{u}_n^\top \\ \end{bmatrix} \end{align*} $$

Now the eigendecomposition becomes:

$$ \begin{equation*} \mathbf{A} = \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_n \\ \end{bmatrix} \begin{bmatrix} \lambda_1\mathbf{u}_1^\top \\ \lambda_2\mathbf{u}_2^\top \\ \ldots \\ \lambda_n\mathbf{u}_n^\top \\ \end{bmatrix} = \lambda_1\mathbf{u}_1\mathbf{u}_1^\top + \lambda_2\mathbf{u}_2\mathbf{u}_2^\top + \ldots + \lambda_n\mathbf{u}_n\mathbf{u}_n^\top \end{equation*} $$

Therefore, the $n \times n$ matrix $\mathbf{A}$ can be broken into $n$ matrices with the same shape ($n \times n$), and each of these matrices has a multiplier which is equal to the corresponding eigenvalue $\lambda_i$. Each of the matrices $\mathbf{u}_i\mathbf{u}_i^\top$ is called a projection matrix.

Imagine that we have a vector $\mathbf{x}$ and a unit vector $\mathbf{v}$. The inner product of $\mathbf{v}$ and $\mathbf{x}$ which is equal to $\mathbf{v} \cdot \mathbf{x} = \mathbf{v}^\top\mathbf{x}$ gives the scalar projection of $\mathbf{x}$ onto $\mathbf{v}$, which is the length of the vector projection of $\mathbf{x}$ into $\mathbf{v}$. If we multiply $\mathbf{v}^\top\mathbf{x}$ by $\mathbf{v}$ again, $\mathbf{v}\mathbf{v}^\top\mathbf{x}$ gives a vector which is called the orthogonal projection of $\mathbf{x}$ onto $\mathbf{v}$. This is shown in Figure 1.

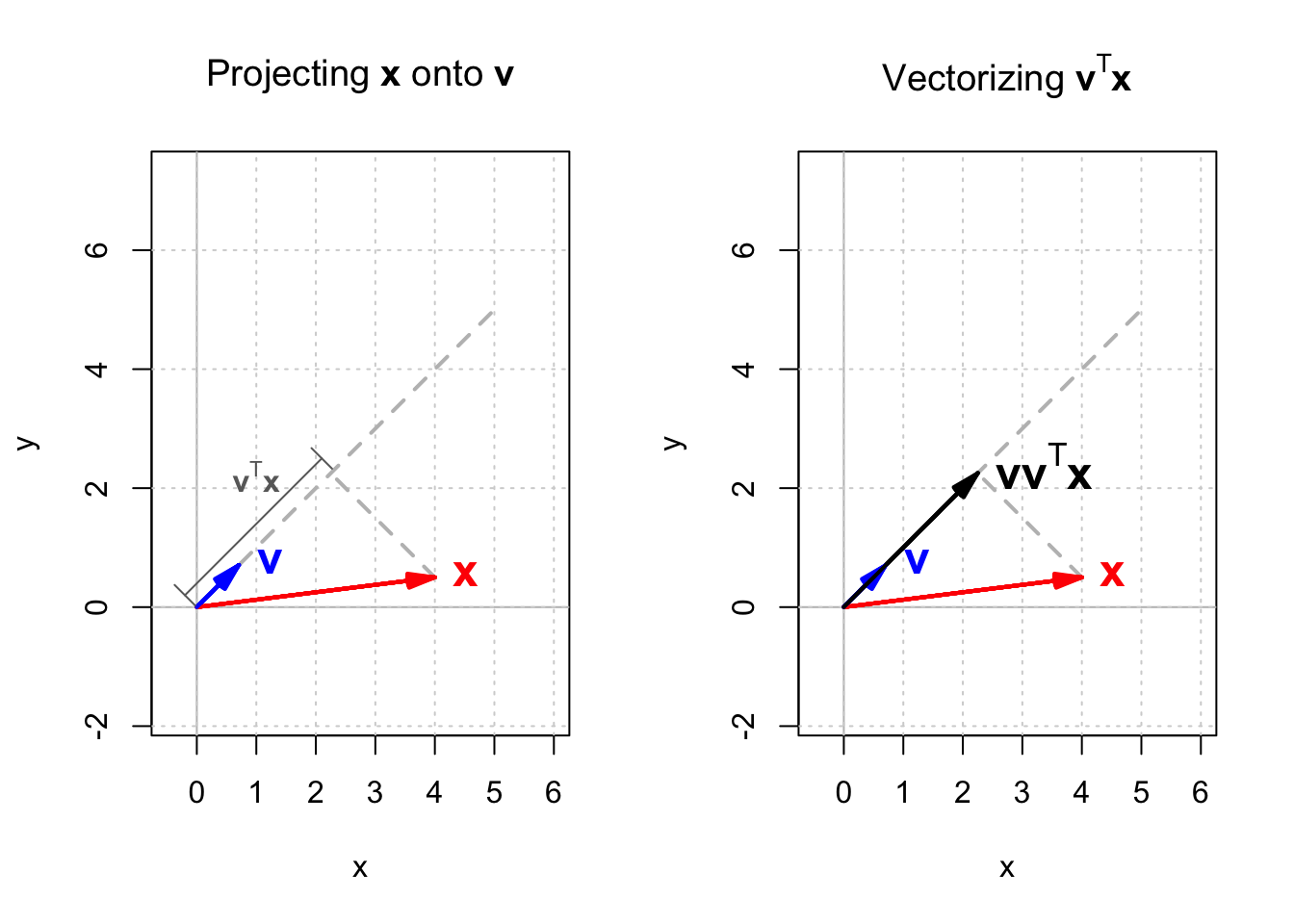
Therefore, when $\mathbf{v}$ is a unit vector, multiplying $\mathbf{v}\mathbf{v}^\top$ by $\mathbf{x}$ will give the orthogonal projection of $\mathbf{x}$ onto $\mathbf{v}$, and that is why $\mathbf{v}\mathbf{v}^\top$ is called the projection matrix. Multiplying $\mathbf{u}_i\mathbf{u}_i^\top$ by $\mathbf{x}$, we get the orthogonal projection of $\mathbf{x}$ onto $\mathbf{u}_i$.

Now let’s use R to calculate the projection matrices of matrix $\mathbf{A}$ mentioned before.

$$ \mathbf{A} = \begin{bmatrix} 3 & 1 \\ 1 & 2 \\ \end{bmatrix} $$

We had already calculated the eigenvalues and eigenvectors of $\mathbf{A}$.

mat_a <- matrix(c(3, 1, 1, 2), 2)
eigen_a <- eigen(mat_a)
eigen_a

eigen() decomposition
$values
[1] 3.618034 1.381966

$vectors
           [,1]       [,2]
[1,] -0.8506508  0.5257311
[2,] -0.5257311 -0.8506508

The next chunk will apply eigendecomposition to $\mathbf{A}$ and print the first term, namely $\mathbf{A}_1$.

u_a <- eigen_a$vectors # an orthogonal matrix made of A's eigenvectors
lambda_a <- eigen_a$values # a vector of A's eigenvalues
mat_a1 <- lambda_a[1] * u_a[,1] %*% t(u_a[,1])
mat_a1 |> round(3)

      [,1]  [,2]
[1,] 2.618 1.618
[2,] 1.618 1.000

$$ \begin{align*} \mathbf{A}_1 &= \lambda_1\mathbf{u}_1\mathbf{u}_1^\top \\ &= 3.618 \begin{bmatrix} -0.851 \\ -0.526 \\ \end{bmatrix} \begin{bmatrix} -0.851 & -0.526 \\ \end{bmatrix} = \begin{bmatrix} 2.618 & 1.618 \\ 1.618 & 1 \\ \end{bmatrix} \end{align*} $$

As you can see, $\mathbf{A}_1$ is also a symmetric matrix. In fact, it can be shown that all projection matrices $\lambda_i\mathbf{u}_i\mathbf{u}_i^\top$ in the eigendecomposition equation are symmetric.

Other than being symmetric, projection matrices have some interesting properties. Let’s continue with $\mathbf{A}_1$ as an example. We can calculate its eigenvalues and eigenvectors:

eigen_a1 <- eigen(mat_a1)
cat("eigenvalues: ", "\n")
ifelse(round(eigen_a1$values, 3) < 0.001, 0, round(eigen_a1$values, 3))
cat("eigenvectors: ", "\n")
eigen_a1$vectors |> round(3)

eigenvalues:  
[1] 3.618 0.000
eigenvectors:  
       [,1]   [,2]
[1,] -0.851  0.526
[2,] -0.526 -0.851

$\mathbf{A}_1$ has two eigenvalues. One is 0. The other one is equal to $\lambda_1$ of the orignal matrix $\mathbf{A}$. In addition, its eigenvectors are identical to that of $\mathbf{A}$. This is not a coincidence. To see why, suppose we multiple $\mathbf{A}_1$ by $\mathbf{u}_1$:

$$ \begin{equation*} \mathbf{A}_1\mathbf{u}_1 = \left( \lambda_1\mathbf{u}_1\mathbf{u}_1^\top \right)\mathbf{u}_1 = \lambda_1\mathbf{u}_1 \left(\mathbf{u}_1^\top\mathbf{u}_1 \right) \end{equation*} $$

We know that $\mathbf{u}_1$ is an eigenvector and it is normalized. Therefore, its length is equal to 1, so is its inner product with itself. Thus we have:

$$ \begin{equation*} \mathbf{A}_1\mathbf{u}_1 = \left( \lambda_1\mathbf{u}_1\mathbf{u}_1^\top \right)\mathbf{u}_1 = \lambda_1\mathbf{u}_1 \end{equation*} $$

Thus, $\mathbf{u}_1$ is an eigenvector of $\mathbf{A}_1$, and the corresponding eigenvalue is $\lambda_1$.

Furthermore,

$$ \begin{equation*} \mathbf{A}_1\mathbf{u}_2 = \left( \lambda_1\mathbf{u}_1\mathbf{u}_1^\top \right)\mathbf{u}_2 = \lambda_1\mathbf{u}_1 \left(\mathbf{u}_1^\top\mathbf{u}_2 \right) \end{equation*} $$

Because $\mathbf{A}$ is symmetric, its eigenvectors $\mathbf{u}_1$ and $\mathbf{u}_2$ are orthogonal, or perpendicular. Given that the inner product of two perpendicular vectors is zero, the inner product of $\mathbf{u}_1$ and $\mathbf{u}_2$ is zero. Thus we have

$$ \begin{equation*} \mathbf{A}_1\mathbf{u}_2 = \left( \lambda_1\mathbf{u}_1\mathbf{u}_1^\top \right)\mathbf{u}_2 = \lambda_1\mathbf{u}_1 \left(\mathbf{u}_1^\top\mathbf{u}_2 \right) \end{equation*} = 0 = 0 \times \mathbf{u}_2 $$

which means that $\mathbf{u}_2$ is also an eigenvector of $\mathbf{A}_1$ and its corresponding eigenvalue is 0, matching the output of eigen_a1$values[2] = 0.

In general, eigendecomposition decomposes a symmetric matrix into $n$ of $n \times n$ projection matrices, $\lambda_i\mathbf{u}_i\mathbf{u}_i^\top$.

Each projection matrix is also symmetric, which shares the same eigenvectors as the original matrix. For a particular project matrix $\lambda_k\mathbf{u}_k\mathbf{u}_k^\top$, the corresponding eigenvalue of eigenvector $\mathbf{u}_k$ is the $k$-th eigenvalue of $\mathbf{A}$, $\lambda_k$, whereas all the remaining eigenvalues are zero.

Recall that a symmetric matrix scales a vector along its eigenvectors, proportionally to the corresponding eigenvalue. Therefore, a projection matrix $\lambda_i\mathbf{u}_i\mathbf{u}_i^\top$ stretches/shrinks a vector along $\mathbf{u}_i$ by $\lambda_i$, but shrinks the vector to zero in all other directions. Let’s illustrate this with $\mathbf{A}$ and one of its projection matrix $\mathbf{A}_1$ in Figure 2.

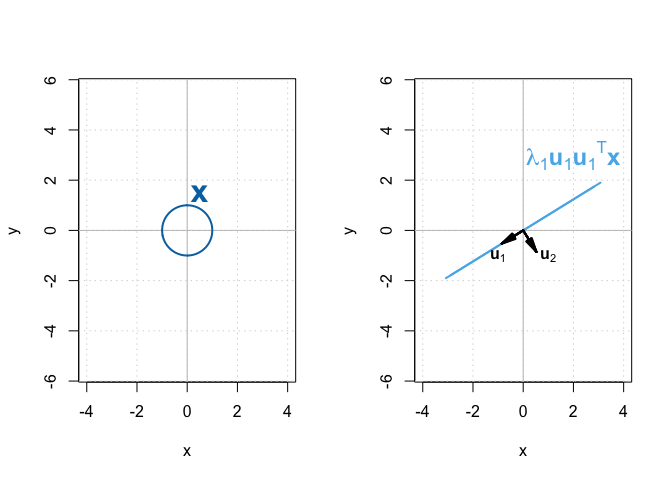
All vectors in $\mathbb{X}$ are transformed by $\mathbf{A}_1$, namely, stretched along $\mathbf{u}_1$ and shrunk to zero along $\mathbf{u}_2$. As a result, the initial circle became a straight line.

Previously, matrix $\mathbf{A}$ transformed vectors in $\mathbb{X}$ into an ellipse, another 2-D shape. And yet, matrix $\mathbf{A}_1$ transformed vectors in $\mathbb{X}$ into a line, a 1-D shape. Both $\mathbf{A}$ and $\mathbf{A}_1$ are symmetric. How come one preserves whereas the other reduces the dimension? In the next post, we will discuss the reason by introducing the concept of rank.